Sie sind hier: [Home] ⊳ [Mathematik] ⊳ [Skalarprodukt]

Skalarprodukt

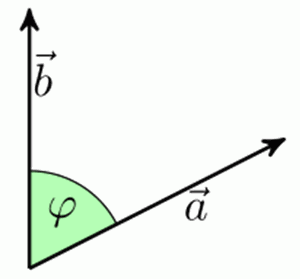
Das Skalarprodukt, das auch als inneres Produkt oder Punktprodukt bezeichnet wird, stellt eine mathematische Verknüpfung dar, bei der zwei Vektoren einer Zahl, einem Skalar, zugeordnet werden. Das Skalarprodukt ist Bestandteil der analytischen Geometrie sowie der linearen Algebra. Geometrisch wird das Skalarprodukt mittels der zwei Vektoren a^→ und b^→ gemäß folgender Formel berechnet: (Hinweis: der Pfeil gehört normalerweise über die Buchstaben, aus Darstellungsgründen steht er nun als "Hochzahl" da).

a^→ ⋅ b^→ = |a^→| |b^→| cos ∢ (a^→, b^→)

Die Bezeichnungen |a^→| |b^→| stehen jeweils für die Längen oder Beträge der beiden Vektoren. Der Kosinus (Winkel) innerhalb der beiden Vektoren wird durch cos ∢ (a, b) = cos φ bezeichnet (φ = phi).

https://de.wikipedia.org/wiki/Skalarprodukt#/media/Datei:Dot-product-1.svg

Berechnung des Skalarprodukts

Wird ein Skalarprodukt errechnet, ist das Ergebnis eine skalare Größe. Das bedeutet, das sich die Größe nur über die Angabe des Zahlenwerts charakterisiert, nach dieser Zahl folgt nichts mehr.

Beispiel: Die Berechnung des Skalarprodukts der folgenden Vektoren

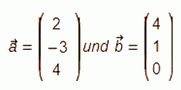
Einsetzen der Vektoren in die Formel

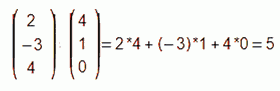
Das Ergebnis ist der Skalar 5

Ohne Rechengesetze oder besser Rechenregeln geht es auch beim Skalarprodukt nicht. Dies sind:

Das Assoziativgesetz (a^→ + b^→) ⋅ c = a^→ ⋅ c + b^→ ⋅ c

Das Distributivgesetz k ⋅ a^→ ⋅ b^→ = a^→ ⋅ (k ⋅ b^→) = (k ⋅ a^→) ⋅ b^→

Das Kommutativgesetz a^→ ⋅ b = b ⋅ a^→

Wo wird das Skalarprodukt angewendet?

Die Geometrie wie auch die Physik sind die Anwendungsfelder für das Skalarprodukt. In der Geometrie natürlich zur Berechnung von Winkeln und in der Physik in einem weit größeren Umfang. Physikalische Größen wie Kraft und Weg sind durch Skalarprodukte definiert.

Worauf führt sich das Skalarprodukt zurück?

Zurückgeführt werden kann das Skalarprodukt auf den griechischen Mathematiker Euklid, der vermutlich im dritten Jahrhundert v. Ch. in Alexandria lebte. Seine Werke über die antike Mathematik waren so umfassend, dass bis heute der sogenannte euklidische Raum als Anschauung dient, um unsere Umwelt mathematisch zu beschreiben. Natürlich ist dieser euklidische Raum heute durch neue Erkenntnisse teils widerlegt, oft aber auch nur erweitert worden, so etwa in Bezug auf die euklidische Geometrie und speziell den euklidischen Vektorraum mit Skalarprodukt.

Fragen und Aufgaben zum Skalarprodukt

1. Was ist ein Skalar?

   Antwort: Eine Zahl

2. Das innere Produkt oder das Skalarprodukt ist aus was eine Multiplikation?

   Antwort: zweier Vektoren

3. Es ist der Vektor a^→ = (2|1|4) gegeben. Mit welchem Vektoren kann man mit a^→ ein Skalarprodukt bilden?

   Antwort: (1|1|1)

4. Welches Skalarprodukt hat das Ergebnis 24?

   Antwort:
   Vektor a^→ hat die Werte a₁ = 4, sowie a₂= 2
   Vektor b^→ hat die Werte b₁ = 4, sowie b₂= 4
   a^→ ⋅ b^→ = a₁ ⋅ b₁ + a₂ ⋅ b₂ = 4 ⋅ 4 + 2 ⋅ 4 = 24

5. Was ist ein sogenannter Zahlentupel?

   Antwort: Der Zahlentupel wird auch Vektor genannt und stellt eine Zahlenreihe dar, dessen richtige Reihenfolge zur Berechnung des Skalarprodukts wichtig ist.

[ © www.quizfragen4kids.de | Quizfragen nicht nur für Kinder | Alle Fragen und Lösungen ohne Gewähr]

↩ Zurück | ↑ Nach oben | Home | Impressum & Kontakt
© www.quizfragen4kids.de