Menu

Quizfragen4Kids | Quizfragen nicht nur für Kinder Quizfragen4Kids.de

Sie sind hier: [Home] ⊳ [Mathematik] ⊳ [L´Hospitalsche Regel]

L´Hospitalsche Regel

Im Jahr 1696 veröffentlichte der französische Mathematiker Guillaume Francois Antoine, Marquise de L’Hospital das erste Lehrbuch zur Differentialrechnung, in dem unter anderem die nach ihm benannte L´Hospitalsche Regel zu finden ist. Die Regel stammt jedoch nicht vom Verfasser L’Hospital, sondern von Johann I. Bernoulli, der sie L’Hospital verkaufte.

Mithilfe dieser Regel ist es möglich, Grenzwerte von Funktionen, die bei zwei bestimmt divergierenden oder gegen Null konvergierenden Funktionen geschrieben werden, über die ersten Ableitungen der Funktionen zu berechnen.

Erklärung:

Ihrem Prinzip nach beruht die L´Hospitalsche Regel darauf, das jedes differenzierbare Funktionspaar f(x) sowie g(x) an den Stellen x0 mittels des jeweiligen, dort befindlichen Tangentenpaars eine Annäherung erlaubt. Die Gleichungen hierzu lassen sich in allgemeiner Form folgendermaßen formulieren:

fr (x|x0) = f’(x0) ∗ (x -x0) + f(x0)

und

gT (x|x0) = g’(x0) ∗ (x -x0) + g(x0)

Anwendung:

Selbst wenn bei Funktionen der Funktionsterm bei der Erreichung der betreffenden Grenze einen unbestimmten Ausdruck liefert, erlaubt es die L´Hospitalsche Regel in den meisten Fällen, den Grenzwert der Funktionen zu bestimmen.

Grundsätzlich alle Anwendungen in der L´Hospitalschen Regel sind auf die Grundaufgabe rückführbar, den Grenzwert limx→x0 f(x) ÷ g(x)

zu bestimmen, insofern dessen Zähler- und Nennerterm limx→x0 f(x) sowie limx→x0 g(x) entweder beide unendlich oder beide null werden und der Quotient f(x) ÷ g(x) ein unbestimmter Ausdruck des Typs ∞ / ∞ oder 0 / 0 ist.

Die Regel umzukehren, funktioniert hingegen nicht. Aus dem Fakt, dass der Grenzwert lim f(x) ÷ g(x) existent ist, ergibt sich nicht zwingend, dass auch lim f'(x) ÷ g(x) existiert

Um die L´Hospitalsche Regel anwenden zu können, muss die Ausgangsfunktion die unbestimmten Ausdrücke ∞ / ∞ oder 0 / 0 liefern, sonst muss sie vorher umgeformt werden, damit sie die Kriterien erfüllt.

Beispiel für: ∞ - ∞

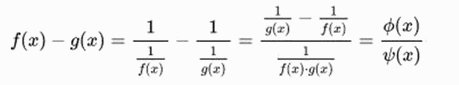
Beispiel für: 0 - ∞

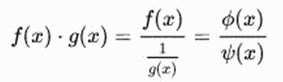
Fragen und Aufgaben zu L´Hospitalsche Regel

  1. Beweisen Sie über den Mittelwertsatz die folgenden Ungleichungen:
    (a) |cos ex -cos ey | = |x -y|für x, y ≤0 ,
    (b) ln(1 + x) ≤x√1 + x für x > 0

    Hinweis zu (b): Betrachten Sie f(t) = ln(1 + t) - t ÷ (√1+t) im Intervall [0, x].

    Antwort:

    (a) Betrachten wir f(t): = cos et auf dem Intervall [x, y] , so liefert der Mittelwertsatz die Relation (cos ex - cos ey)÷ (x-y) = f'(t0)

    für ein gewisses, aber nicht bekanntes t0 ∈ [x, y].

    Also ist |cos ex − sin ey|= |f'(t0) | |x − y|

    und damit |cos ex − sin ey| ≤ |x − y|maxt0∈ [x,y] |f'(t0) |.

    Es bleibt daher zu zeigen, dass |f'(t) | ≤1 ist für alle t ∈ [x, y]. Nun ist |f'(t) |= | − et sin et|= |et| × |sin t|.

    Der zweite Faktor ist stets ≤1, der erste Faktor ebenso, weil t negativ ist.

    (b) Wir haben
    f(x) -f(0)
    x -0 = f'(t0)
    für ein gewisses t0 ∈[0, x], also f(x) = x f'(t0)). Wir erhalten
    f'(t) = 1
    1 + t - 1√1 + t + t 1
    2 (1 + t)3/2 =
    √1 + t -(1 + t/2)
    (1 + t) √1 + t .

    Der Nenner ist positiv, der Zähler wegen 1 + t/2 =√1 + t (Bernoulli’sche Ungleichung) negativ. Daher ist in (*) die gesamte rechte Seite negativ und somit f(x) < 0, und die Behauptung ist bewiesen.

  2. Berechnen Sie folgende Grenzwerte:

    und bestimmen Sie die Konstante c ?R so, dass die Funktion f(x) =

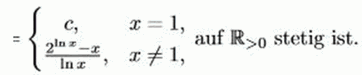
    Antwort:

    a) Teil (i): Wir haben mit einem Grenzwert “ ∞: ∞ zu tun, den wir durch mehrmaliges Anwenden der Regel von l’Hospital berechnen.

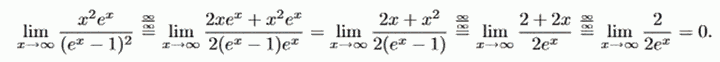
    Teil(ii): Hier liegt ein Grenzwert vom Typ 0 vor

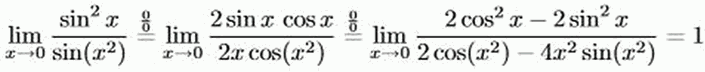
    (b) Als Quotient stetiger Funktionen ist f für alle x ∈ ℝ >0 \{1} stetig. Es ist also c so zu bestimmen, dass f in 1 stetig ist, dass also gilt

    Zunächst formen wir den Ausdruck im Grenzwert noch ein wenig um:

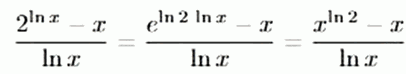
    Auch hier haben also mit einem Grenzwert vom Typ “0 ” zu tun.

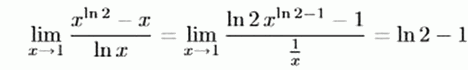
    Mit der Wahl c = ln 2 -1 ist also f auf ℝ >0 stetig.

  3. Es soll die Taylor-Formel zweiter Ordnung verwendet werden, mit dem Entwicklungspunkt x0 = 0 sowie dem Langrangeschen Restglied um die Einschließung

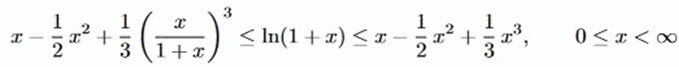
    zu beweisen.

    Antwort: Sei f(x) = ln(1 + x). Dann gilt

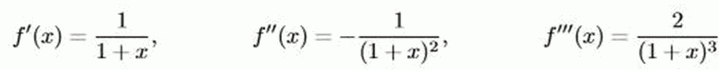
    Mit der Taylor-Formel an der Entwicklungsstelle 0 erhalten wir damit

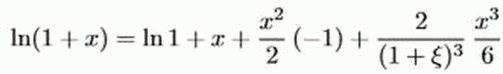
    mit einem ξ ∈ (0, x). Für das Restglied gilt nun die folgende Ungleichung


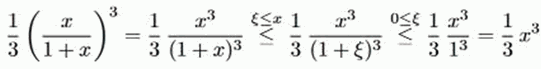
[ © www.quizfragen4kids.de | Quizfragen nicht nur für Kinder | Alle Fragen und Lösungen ohne Gewähr]

↩ Zurück | ↑ Nach oben | Home | Impressum & Kontakt
© www.quizfragen4kids.de