Sie sind hier: [Home] ⊳ [Mathematik] ⊳ [Krümmungsverhalten]

Krümmungsverhalten

Krümmung ist ein mathematischer Begriff und beschreibt in seiner einfachsten Bedeutung die lokale Abweichung einer Kurve von einer Geraden. Der gleiche Begriff steht ebenso für das Krümmungsmaß, das quantifiziert, wie stark die lokale Abweichung an jedem Punkt der Kurve ist. Basierend auf dem Begriff Krümmung der Kurve kann die Krümmung der Oberfläche im dreidimensionalen Raum beschrieben werden, indem die Krümmung der Kurve auf der Oberfläche untersucht wird. Ein bestimmter Teil der Krümmungsinformationen, nämlich die Gaußsche Krümmung, hängt einzig von der inneren Geometrie einer Fläche ab, d.h. es ist von der ersten Grundform (oder des metrischen Tensors) abhängig, wie die Bogenlänge der Kurve berechnet wird.

Dieses Konzept der intrinsischen Krümmung kann auf Mannigfaltigkeiten mit jeder metrischen Tensor Dimension erweitert werden. Diese Varietät erklärt die parallele Übertragung entlang der Kurve, und die Krümmungsvariable gibt an, wie stark sich die Richtung des Vektors nach einer Umdrehung ändert, wenn er parallel entlang der geschlossenen Kurve übertragen wird. Zu den Anwendungen bezüglich des Krümmungsverhalten gehört Albert Einsteins Allgemeine Relativitätstheorie, die Gravitation als Krümmung der Raumzeit beschreibt.

In der Geometrie ist die Krümmung einer ebenen Kurve die Richtungsänderung, während sie sich durch die Kurve bewegt. Die Krümmung von Geraden ist überall Null, da sich die Richtung nicht ändert.

Zur Definition einer Krümmung in einer beliebigen Kurve an einem Punkt ist die Betrachtung eines Kurvenstücks der Länge ?s notwendig, in dem der fragliche Punkt enthalten ist und bei dem sich die Tangenten in den Endpunkten im Winkel ?l überschneiden.

Definition der Krümmung k in dem Punkt:

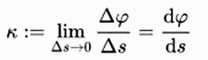
Wenn die Krümmung eines Punktes nicht Null ist, wird der Kehrwert der Krümmung als Krümmungsradius bezeichnet; Dies ist der Radius des Krümmungskreises, der durch diesen Punkt geht, d. h. der Kreis, der dem Krümmungspunkt am nächsten liegt. Er wird hier Krümmungsmittelpunkt genannt und kann gebildet werden, indem man den Krümmungsradius senkrecht zur Tangente der Kurve in die Richtung der Kurvenkrümmung abträgt.

Wendestelle oder Wendepunkte

Wenn sich eine Krümmung ändert, entsteht am Beginn der Änderung ein Wendepunkt oder eine Wendestelle.

Zur Berechnung von Wendepunkten muss die 2. Ableitung der Funktion bestimmt werden. Die Nullstellen in der 2. Ableitung stellen die x-Koordinaten der Wendepunkte dar. Zur Bestimmung der y-Koordinaten müssen die x-Koordinaten in ihre ursprüngliche Funktion eingesetzt werden. Weiterführend kann nun festgestellt werden, ob der Wendepunkt Rechts-Links oder Links-Rechts verläuft. Dazu wird die 3. Ableitung aus der 2. Ableitung bestimmt. Nun wird x durch die x-Koordinate des Wendepunktes in die 3. Ableitung eingesetzt. Das Ergebnis kann nun folgendermaßen aussehen:

• f'''(x)>0 rechts-linksgekrümmt
• f'''(x)<0 links-rechtsgekrümmt
• f'''(x)=0 es liegt KEIN Wendepunkt vor

Nachfolgend eine Grafik mit einem Krümmungsverhalten, das einen Wendepunkte beinhaltet, der den Kurvenverlauf von einer Rechtskrümmung in eine Linkskrümmung verändert:

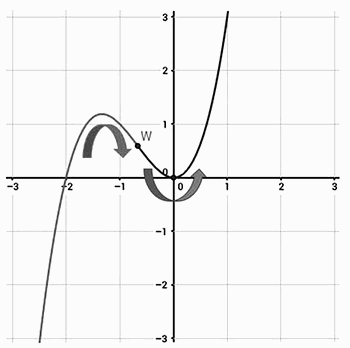
Der mit „W“ bezeichnete Punkt ist der Wendepunkt.

Fragen und Aufgaben zum Krümmungsverhalten

1. Berechne den Wendepunkt der Funktion: f(x) = x³+3x²

   Antwort: Erste und zweite Ableitung berechnen:
   f'(x)=3x²+6x
   f''(x)=6x+6

   Nullstellen der 2. Ableitung berechnen:
   0=6x+6
   x=-1

   y-Koordinate des Wendepunktes bestimmen:
   y = -1³+3× (-1)² = 2
   entsprechend besitzt der Wendepunkt die Koordinaten W(-1|2)

   Bestimmung der 3. Ableitung
   f'''(x)=6
   Ergebnis: Es ist ein rechts-links Wendepunkt

2. Bestimme das Krümmungsverhalten der folgenden Funktion f (x) = x³ + 2x²

   Antwort: Erste und zweite Ableitung berechnen: f'(x) = 3x² + 4x
   f''(x) = 6x + 4

   Die Nullstellen der 2. Ableitung bestimmen:
   0= 6x + 4
   x = – 2/3
   f''(-1) = -6 + 4 = -2
   f''(1) = 6 + 4 = 10
   Ergebnis: die Funktion besitzt eine Rechts-Links-Krümmung

[ © www.quizfragen4kids.de | Quizfragen nicht nur für Kinder | Alle Fragen und Lösungen ohne Gewähr]

↩ Zurück | ↑ Nach oben | Home | Impressum & Kontakt
© www.quizfragen4kids.de