Quizfragen4Kids | Quizfragen nicht nur für Kinder

Sie sind hier: [Home] ⊳ [Mathematik] ⊳ [Baumdiagramme]

Baumdiagramme

Baumdiagramme dienen innerhalb der Mathematik zur Berechnung von mehrstufigen Wahrscheinlichkeitsproblemen. Dabei gilt es, zwei wichtige Regeln zu beachten:

1. Für die Berechnung einer Wahrscheinlichkeit werden alle Wahrscheinlichkeiten entlang eines Pfades, der zum Ergebnis führt, miteinander multipliziert.

2. Besteht das Baumdiagramm eines Ereignisses aus mehreren Pfaden, werden die Ergebniswahrscheinlichkeiten der Pfade miteinander addiert.

Anhand zweier einfacher Beispiele lässt sich das Baumdiagramm zur Berechnung von Wahrscheinlichkeiten erklären:

In einer Vase befinden sich 4 Kugeln, 2 Schwarze (S) und 2 Weiße (W). Im ersten Beispiel werden nun nacheinander zwei Kugeln gezogen und nach dem Ziehen sofort wieder zurückgelegt. Bei jedem Zug ist also immer die selbe Anzahl Kugeln in der Vase.

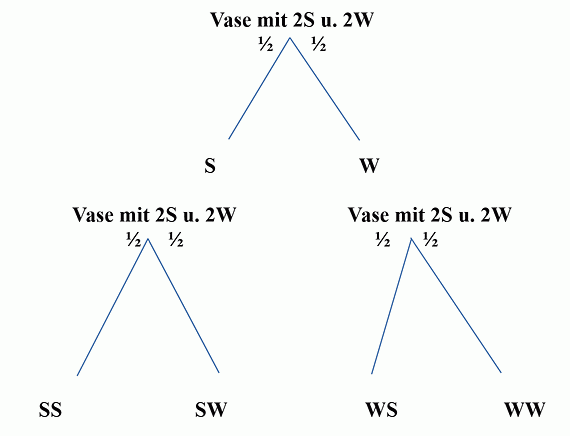
Baumdiagramm

Im zweiten Beispiel werden die Kugeln ebenfalls gezogen, aber nicht mehr zurückgelegt:

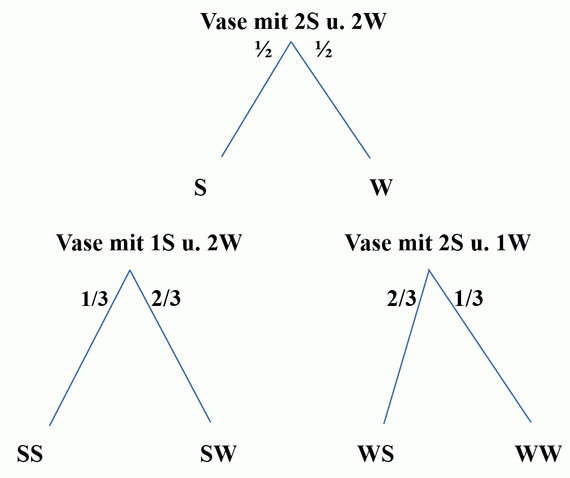
Baumdiagramm

im ersten Beispiel mit zurücklegen werden als Ereignis (E) eine weiße und eine schwarze Kugel gezogen

Die Wahrscheinlichkeit P (E) für dieses Ereignis ist

P (E) = P (SW) + P (WS) = ½ × ½ + ½ × ½ = ½

Ohne zurücklegen sieht die Wahrscheinlichkeit so aus:

P (E) = P (SW) + P (WS) = ½ × &frac23; + ½ × &frac23; = &frac23;

Fragen und Aufgaben zum Baumdiagramm

Eine Vase enthält 10 Kugeln. Davon sind 5 blau (B), 3 rot (R) und 2 gelb (G). Nacheinander werden drei Kugeln gezogen und jede gezogene Kugel sofort wieder zurückgelegt. Wie hoch ist die Wahrscheinlichkeit, dass die 3 gezogenen Kugeln unterschiedliche Farben haben, also je eine blaue, eine rote und eine gelbe Kugel gezogen wird?

Antwort: Es gilt, das 6 Wahrscheinlichkeiten für die Annahme möglich sind, das drei verschiedenfarbene Kugeln gezogen werden
P(E) = P(BRG) + P(BGR) + P(RBG) + P(RGB) + P(GBR) + P(GRB)

Die Wahrscheinlichkeit P für dieses Ereignis lässt sich folgendermaßen berechnen
P (BRG) = 5/10 × 3/10 × 2/10 = 30/1000 = 3/100
daraus ergibt sich
P (E) = 6 × 3/100 = 9/50

Die Wahrscheinlichkeit, dass 3 verschiedenfarbige Kugeln gezogen werden, liegt also bei 9 von 50.
Wie hoch ist die Wahrscheinlichkeit dreier verschiedener Farben aus der vorhergehenden Frage, wenn die Kugeln nach dem Ziehen nicht wieder zurückgelegt werden?

Antwort: P (BRG) = 5/10 × 3/9 × 2/8 = 1/24
P (E) = 1/12 + 1/120 + 0 = 11/120

Ohne zurücklegen der Kugeln verringert sich die Wahrscheinlichkeit, dass drei verschiedene Farben gezogen werden, noch einmal deutlich auf 11 von 120.

Baumdiagramme

Fragen und Aufgaben zum Baumdiagramm

Wie hoch ist die Wahrscheinlichkeit dreier verschiedener Farben aus der vorhergehenden Frage, wenn die Kugeln nach dem Ziehen nicht wieder zurückgelegt werden?